算法入门之初级排序 | GeniusFunny的个人博客

算法入门之初级排序

GeniusFunny 10月 03, 2018

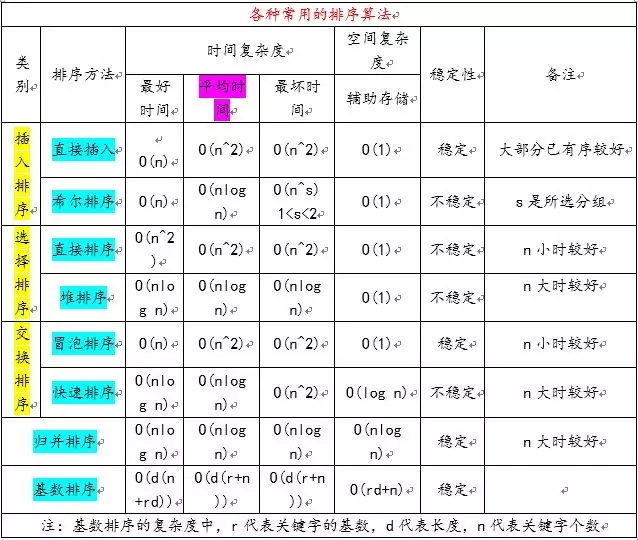
稳定性指排序前后两个相等的数相对位置不变，则算法稳定；

稳定排序：基数排序、冒泡排序、插入排序、归并排序

非稳定排序：堆排序、快速排序、希尔排序、选择排序

下面是常见排序的简单介绍及实现。

冒泡排序

稳定排序
小的元素往前调或者把大的元素往后调；
比较是相邻的两个元素比较，交换也发生在这两个元素之间；

实现：

function bubbleSort(arr) {
  // 遍历数组，若当前元素大于右边的元素，则二者交换位置，较大的元素继续往后比较
  // 若当前元素小于右边的元素，则以右边的元素开始继续往后方比较
  // 表现：大元素逐渐冒泡到数组后方
  const len = arr.length;
  for(let i = len; i > 0; i--) {
    for(let j = 1; j < i; j++) {
      if (arr[j] < arr[j-1]) {
        let temp = arr[j-1];
        arr[j-1] = arr[j]
        arr[j] = temp;
      }
    }
  }
  console.log(arr)
}

选择排序

不稳定排序
每个位置选择当前元素最小的；
在一趟选择中，如果当前元素比一个元素小，而该小的元素又出现在一个和当前元素相等的元素后面，那么交换后稳定性就被破坏了；

实现：

function selectSort(arr) {
  const len = arr.length;
  for(let i = len - 1; i > 0; i--) {
    for(let j = 0; j < i; j++) {
      if (arr[i] < arr[j]) {
        let temp = arr[j];
        arr[j] = arr[i];
        arr[i] = temp;
      }
    }
  }
}

插入排序

已经有序的小序列的基础上，一次插入一个元素；
想要插入的元素和已经有序的最大者开始比起，如果比它大则直接插入在其后面，否则一直往前找直到找到它该插入的位置；
如果碰见一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面；

实现

function insertSort(arr) {
  const len = arr.length;
  for(let i = 1; i < len; i++) {
    for(let j = i; j >= 0; j--) {
      if (arr[j] < arr[j-1]) {
        let temp = arr[j];
        arr[j] = arr[j-1];
        arr[j-1] = temp;
      }
    } 
  }
}

希尔排序

按照不同步长对元素进行插入排序；
当刚开始元素很无序的时候，步长最大，所以插入排序的元素个数很少，速度很快；
当元素基本有序了，步长很小，插入排序对于有序的序列效率很高；

由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱；

function shellSort(arr, gapArr) {
  const len = arr.length;
  for(let k = 0; k < gapArr.length; k++) {
    let gap = gapArr[k];
    for(let i = gap; i < len; i++) {
      for(let j = i; j >= 0; j -= gap) {
        if (arr[j] < arr[j-gap]) {
          let temp = arr[j];
          arr[j] = arr[j-gap];
          arr[j-gap] = temp;
        }
      }
    }
  }
}

快速排序

首先，从数组中选择中间一项作为主元
创建两个指针，左边一个指向数组第一个项，右边一个指向数组最后一个项。
- 移动左指针直到我们找到一个比主元大的元素，接着，移动右指针直到找到一个比主元小的元素，然后交换它们
- 重复这个过程，直到左指针超过了右指针；这个过程将使得比主元小的值都排在主元之前，而比主元大的值都排在主元之后。这一步叫作划分操作。
接着，算法对划分后的小数组(较主元小的值组成的子数组，以及较主元大的值组成的子数组)重复之前的两个步骤，直至数组已完全排序。

不稳定发生在中枢元素和a[j] 交换的时刻；

function quickSort(arr) {
  function partition(arr, left, right) {
    let pivot = arr[Math.floor((left+right) / 2)];
    let i = left, j = right;
    while(i <= j) {
      while(arr[i] < pivot) i++
      while(pivot < arr[j]) j--
      if (i <= j) {
        [arr[i], arr[j]] = [arr[j], arr[i]];
        i++
        j--
      }
    }
    return i;
  }
  function qSort(arr, left, right) {
    let pivot
    if (left < right) {
      pivot = partition(arr, left, right);
      if (left < pivot-1) qSort(arr, left, pivot-1)
      if (right > pivot) qSort(arr, pivot, right)
    }
  }
  qSort(arr, 0, arr.length-1)
}

枢纽元的选择：

固定首位或末位
随机选择
三数中值法，首、尾、中间选择中间值

快排的优化：

当待排序序列的长度分割到一定大小后，使用插入排序。
在一次分割结束后，可以把与Key相等的元素聚在一起，继续下次分割时，不用再对与key相等元素分割
在一次分割结束后，将与本次基准相等的元素聚集在一起，再分割时，不再对聚集过的元素进行分割。具体过程有两步
- 在划分过程中将与基准值相等的元素放入数组两端。
- 划分结束后，再将两端的元素移到基准值周围。
优化递归操作，尾递归优化
“优化不必要的交换”

归并排序

把序列递归地分成短序列，递归出口是短序列只有1个元素(认为直接有序)或者2个序列(1次比较和交换),然后把各个有序的短序列合并成一个有序的长序列，不断合并直到原序列全部排好序；
合并过程中我们可以保证如果两个当前元素相等时，我们把处在前面的序列的元素保存在结果序列的前面，这样就保证了稳定性；

非原地归并

function mergeSort(arr) {
  function innerMergeSort(arr) {
    const len = arr.length;
    if (len === 1) return arr;
    let mid = Math.floor(len / 2), left = arr.slice(0, mid), right = arr.slice(mid, len);
    return merge(innerMergeSort(left), innerMergeSort(right));
  }
  function merge(left, right) {
    const result = [];
    let i = 0, j = 0;
    const leftLength = left.length;
    const rightLength = right.length;
    while(i < leftLength && j < rightLength) {
      if (left[i] < right[j]) result.push(left[i++])
      else result.push(right[j++])
    }
    while(i < leftLength) {
      result.push(left[i++])
    }
    while(j < rightLength) {
      result.push(right[j++])
    }
    return result;
  }
  return innerMergeSort(arr)
}

原地归并

function mergeSort(arr) {
  let aux = [] // 辅助数组
  function innerMergeSort(arr, left, right) {
    if (right - left > 1) {
      let mid = Math.floor((right + left) / 2);
      console.log(left, mid, right)
      innerMergeSort(arr, left, mid);
      innerMergeSort(arr, mid+1, right);
      merge(arr, left, mid, right);
    } else if(right - left === 1) {
      if (arr[left] > arr[right]) [arr[left], arr[right]] = [arr[right], arr[left]]
    }
  }
  function merge(arr, left, mid, right) {
    let i = left, j = mid+1
    for(let k = left; k <= right; k++)
      aux[k] = arr[k]
    for(let k = left; k <= right; k++) {
      if (i > mid) arr[k] = aux[j++] // 左半边用尽（取用右半边的元素）
      else if(j > right) arr[k] = aux[i++] // 右半边用尽（取用左半边的元素）
      else if(aux[i] < aux[j]) arr[k] = aux[i++] // 左半边当前元素小于右半边当前元素（取用左半边的元素）
      else arr[k] = aux[j++] // // 左半边当前元素大于右半边当前元素（取用右半边的元素）
    }
  }
  innerMergeSort(arr, 0, arr.length-1)
}

基数排序

按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位；
有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序，最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前；
用于整数；
需要较多的存储空间；
基于分别排序，分别收集；

堆排序

堆的性质
- 完全二叉树
- 每个节点的值大于或等于其右左孩子节点【大顶堆】；反之，小顶堆
- 节点i的孩子为2i和2i+1节点，大顶堆要求父节点大于等于其2个子节点；小顶堆要求父节点小于等于其2个子节点
堆排序：选择排序的一种
- 将待排序的序列构造成一个大顶堆，此时整个序列的最大值就是堆顶的根节点。
- 将其与堆数组末尾元素交换，再将剩余的n-1个序列重新构成一个堆，这样就得到n个元素的次大值；反复执行，就能得到一个有序序列了。

实现

构造堆
输出堆顶元素后，调整剩余元素成为一个新的堆

function heapSort(arr) {
  let heapSize = arr.length;
  buildHeap(arr);
  while(heapSize > 1) {
    heapSize--;
    [arr[0], arr[heapSize]] = [arr[heapSize], arr[0]]
    heapify(arr, heapSize, 0)
  }
  function buildHeap(arr) {
    // 处理有子节点的节点
    for(let i = Math.floor(arr.length / 2); i >= 0; i--) {
      heapify(arr, heapSize, i)
    }
  }
  // 保证 arr[parent] > arr[parent*2+1]与arr[parent*2+2]
  function heapify(arr, heapSize, i) {
    let left = 2*i+1, right = 2*i+2;
    let largest = i;

    if (left < heapSize && arr[left] > arr[largest]) largest = left;
    if (right < heapSize && arr[right] > arr[largest]) largest = right;
    if (largest !== i) {
      [arr[i], arr[largest]] = [arr[largest], arr[i]];
      // 交换根节点与最大节点的位置，根节点的值可能小于其子节点 需要再来一次heapify
      heapify(arr, heapSize, largest)
    }
  }
}

###